In graph theory, the degree of a vertex is the number of edges connected to it. In this article, we will study the degree of a vertex in a graph with its definition, examples, and related theorems, such as Handshaking lemma.
Degree of a Vertex
Definition: In an undirected graph, the number of edges connected to a vertex is called the degree of that vertex.
A loop at a vertex contributes twice to the degree of that vertex.
The degree of a vertex v in a graph G is denoted by deg(v).
Examples
Let us consider the following graph.
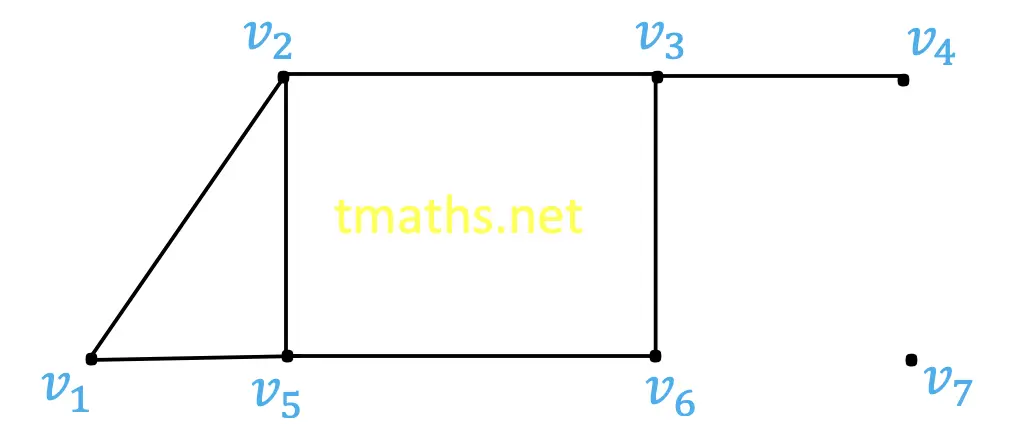
In the above graph, we observe that there are two edges connected to v1 and there are three edges connected to v2. Therefore,
deg(v1) = 2 and deg(v2) = 3.
Similarly, deg(v3) = 3, deg(v4) = 1, deg(v5) = 3, deg(v6) = 2, deg(v7) = 0.
Thus, v4 is a pendant vertex and v7 is an isolated vertex.
Properties
The degree of a vertex of a graph has the following properties.
- The degree of an isolated vertex is 0.
- If a vertex has a loop incident with it, then it contributes twice to the degree of the vertex.
- If the degree of a vertex is 1, then it is called a pendant vertex.
- The sum of the degrees of all vertices is equal to two times the number of edges. This is known as the Sum of Degree Theorem.
- In an undirected graph, the number of vertices of odd degree is even.
Handshaking Theorem
Statement: If G=(V, E) is an undirected graph having e edges, then we have
That is, the sum of the degrees of all vertices = 2 times the number of edges. This Theorem is also known as the Degree Sum Theorem or the Handshaking Lemma.
Proof of Handshaking Theorem
We know that each edge is connected with exactly two vertices. This ensures that each edge contributes 2 to the sum of the degrees of all vertices.
Therefore, it follows that
This completes the proof of the Handshaking Theorem.
Theorem
Prove that the number of vertices of odd degree in a graph is always even.
Proof:
Let G = (V, E) be an undirected graph.
Let us consider the two sets defined by
V1:= The set of vertices of G of even degree.
V2:= The set of vertices of G of odd degree.
By Handshaking theorem, we have
⇒ |
By definition, the sum
As each deg(vi) is odd, for each vi ∈ V2,
Also Read:
- Simple graph with n vertices has a pair of vertices of same degree
- Prove that a tree with n vertices has (n-1) edges
- Simple Graph with n Vertices and k Components have at most (n-k)(n-k+1)/2 Edges
Homepage of Discrete Mathematics
FAQs
Q1: What is handshaking lemma?
Answer: The handshaking lemma states that the sum of the degrees of all vertices in a graph is equal to 2 times the number of edges.
This article is written by Dr. Tathagata Mandal, Ph.D in Mathematics from IISER Pune (Algebraic Number Theory), Postdocs at IIT Kanpur & ISI Kolkata. Currently, working as an Assistant Prof. at Adamas University. Thank you for visiting the website.