The nth derivative of a function f(x) is obtained by by successively differentiating f(x) n times with respect to x. The Leibnitz theorem is a powerful tool to find it for a product function. In this post, we will learn how to find n-th derivative of a function with examples.
Definition of nth Derivative
The first order derivative of f(x) is denoted by $f'(x)$, and it is given by the limit: $f'(x)=\lim\limits_{h \to 0}$ $\dfrac{f(x+h)-f(x)}{h}$.
The n-th order derivative of f(x) is denoted by f(n)(x) and it is obtained by differentiating f(n-1)(x) with respect to x. So we have:
$f^{(n)}(x)=\lim\limits_{h \to 0}$ $\dfrac{f^{(n-1)}(x+h)-f^{(n-1)}(x)}{h}$.
Notation: The nth derivative of $y$ is usually denoted by $y_n$.
Examples of nth Derivative
nth order derivative of xn
Question: Find the nth order derivative of f(x)=xn.
Answer:
Here f(x)=xn.
By the power rule of differentiation, we have that
| $f'(x)=nx^{n-1}$ $f^{”}(x)=n(n-1)x^{n-2}$ $f^{”’}(x)=n(n-1)(n-2)x^{n-3}$ |
So the kth order derivative of f(x)=xn is given by
$f^{(k)}(x)=n(n-1)…(n-k+1)x^{n-k}$.
Thus, to obtain the nth order derivative, let us put k=n here. As a result we obtain that
$f^{(n)}(x)=n(n-1)…(n-n+1)x^{n-n}$
⇒ $f^{(n)}(x)=n(n-1)…1$ as we know x0=1.
⇒ $f^{(n)}(x)=n!$
So the nth order derivative of xn is equal to n!.
Remark: The mth order derivative of f(x)=xn is given by
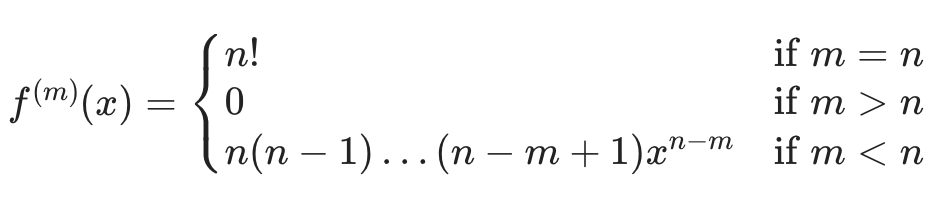
nth Derivative of sinx
Question: Find the nth order derivative of sinx.
Answer:
Here f(x)=sinx.
The first derivative is given by
$f'(x)=\cos x$
⇒ $f'(x)=\sin(\frac{\pi}{2}+x)$
In a similar way, we obtain that
| $f^{”}(x)=\cos(\frac{\pi}{2}+x)$ $f^{”}(x)= \sin(\frac{\pi}{2}+\frac{\pi}{2}+x)$ using the formula sin(π/2 +θ) = cosθ. ⇒ $f^{”}(x) = \sin(2 \cdot \frac{\pi}{2}+x)$ |
Also, we have:
| $f^{(3)}(x)=\cos(2 \cdot \frac{\pi}{2}+x)$ $f^{(3)}(x)= \sin(\frac{\pi}{2}+2\cdot \frac{\pi}{2}+\frac{\pi}{2}+x)$ as we know sin(π/2 +θ) = cosθ. ⇒ $f^{(3)}(x) = \sin(3 \frac{\pi}{2}+x)$ |
Observing the patterns, we see that $f^{(n)}(x) = \sin(n \cdot \frac{\pi}{2}+x)$.
So the nth derivative of sinx is equal to sin(nπ/2 +x).
Note:
- The nth derivative of sin(ax+b) is equal to an sin(nπ/2 +ax+b).
- In a similar way, the derivative of cosx is equal to cos(nπ/2 +x). Also, the nth derivative of cos(ax+b) is equal to an cos(nπ/2 +ax+b).
nth Derivative of 1/x
Question: Find the nth order derivative of $\dfrac{1}{x}$.
Answer:
Here f(x)= 1/x = x-1.
| So f'(x) = -1 ⋅ x-1-1 = -1 ⋅ x-2 f”(x) = -1 ⋅ -2 x-2-1 = -1 ⋅ -2 x-3 f”'(x) = -1 ⋅ -2 ⋅ -3 x-3-1 = -1 ⋅ -2 ⋅ -3 x-4 |
Therefore, we observe that
f(n)(x) = -1 ⋅ -2 ⋅ -3 ⋅⋅⋅ -n x-n-1 = (-1)n 1⋅ 2 ⋅ 3⋅n x-(n+1)
⇒ f(n)(x) = $\dfrac{(-1)^n n!}{x^{n+1}}$.
So the nth derivative of 1/x is equal to (-1)n n! x-(n+1).
nth Derivative of logx
Question: Find the nth order derivative of logx.
Answer:
Here f(x)=log x.
Differentiating with respect to x, we get that
f'(x) = $\dfrac{1}{x}$.
Differentiating it (n-1) times w.r.t x using the rule in Q3, we obtain the nth order derivative of f(x) = 1/x which is given below:
f(n)(x) = $\dfrac{(-1)^{n-1} (n-1)!}{x^n}$.
So the nth order derivative of logx is equal to (-1)n-1 (n-1)! x-n.
Leibnitz Theorem
Statement: For two continuously differentiable functions u and v, the nth order derivative of the product uv is given by the following formula:
(uv)n = unv + nc1 un-1v1 + nc2 un-2v2 + … + uvn.
Application
| Q1: Find the nth derivative of y = ex logx. |
Answer:
y = ex logx
Put u=ex and v=log x.
∴ un = ex and vn = $\dfrac{(-1)^{n-1}(n-1)!}{x^n}$.
Therefor, by Leibnitz’s theorem, the nth order derivative of y = ex logx is given by
yn = ex ⋅ log x + nc1 ⋅ ex ⋅$\dfrac{1}{x}$ + nc2 ⋅ ex $\left( -\dfrac{1}{x^2}\right)$ + … + ex $\dfrac{(-1)^{n-1}(n-1)!}{x^n}$
⇒ yn = ex { log x + nx-1 + nc2 x-2 + … + (-1)n-1 (n-1)! x-n }.
| Q2: If y = tan-1x, then show that (1+x2)yn+1 +2nxyn +n(n-1)yn-1 = 0. |
Answer:
Differentiating the both sides with respect to x, we have that
y1 = $\dfrac{1}{1+x^2}$
⇒ (1+x2)y1 = 1
Let us now differentiate n-times with respect to x. This gives us that
[y1(1+x2)]n = (1)n
⇒ yn+1(1+x2) + nc1 yn ⋅2x + nc2 yn-1 ⋅2 = 0
⇒ (1+x2)yn+1 + 2nxyn + n(n-1)yn-1 = 0, this completes the proof.
| Q3: If y = em sin-1x, then prove that (1-x2)yn+2 – (2n+1)xyn+1 -(n2+m2)yn = 0, where yn denotes the nth derivative of y. |
Answer:
y = em sin-1x.
Differentiate both sides with respect to x. So we have that
y1 = $e^{m \sin^{-1}x} \times \dfrac{m}{\sqrt{1-x^2}}$
Cross-multiplying, we get that
y12(1-x2) = m2y2.
If we differentiate again with respect to x, we obtain that
2y1 y2(1-x2) +y12 ⋅(-2x) = m2⋅2yy1
Cancelling 2y1, we have: y2 (1-x2) – xy1 = m2y.
Now, we differentiate using Leibnitz’s rule, it follows that
| yn+2 (1-x2) + nc1 yn+1 ⋅(-2x) + nc1 yn ⋅(-2) – {yn+1x + nc1 yn ⋅1} = m2yn ⇒ (1-x2)yn+2 – 2nxyn+1 – n(n-1)yn – xn+1 – nyn = m2yn |
Therefore, (1-x2)yn+2 – (2n+1)xyn+1 -(n2+m2)yn = 0.
This article is written by Dr. Tathagata Mandal, Ph.D in Mathematics from IISER Pune (Algebraic Number Theory), Postdocs at IIT Kanpur & ISI Kolkata. Currently, working as an Assistant Prof. at Adamas University. Thank you for visiting the website.